- Регистрация
- 17 Авг 2024
- Сообщения
- 19
- Реакции
- 22
- Баллы
- 8
Парадокс дней рождения — это удивительный пример того, как наша интуиция часто ошибается в оценке вероятностей. Казалось бы, чтобы шанс совпадения дней рождения у двух человек стал больше 50%, нужно собрать очень много людей. Ведь в году 365 дней, и можно подумать, что для такого совпадения понадобится хотя бы половина этого числа. Но реальность оказывается совсем другой.
Суть в том, что вероятность совпадения растет гораздо быстрее, чем мы ожидаем. Вместо прямого подсчета шансов совпадения проще посчитать вероятность обратного — что у всех дни рождения разные. Для первого человека вероятность уникальности равна 100%, ведь других пока нет. Для второго — 364 из 365, потому что один день уже занят. Для третьего — 363 из 365, и так далее.
Если взять группу из 23 человек, то вероятность того, что все дни рождения разные, вычисляется как последовательное умножение: 365 умножить на 364, затем на 363, и так до 343, разделив каждый раз на 365. В итоге получается примерно 0,493, то есть 49,3%. Значит, вероятность хотя бы одного совпадения — это 100% минус 49,3%, то есть около 50,7%.
Почему так происходит? Дело в том, что с ростом числа людей количество возможных пар растет очень быстро. В группе из 23 человек можно составить 253 уникальные пары. Хотя шанс совпадения для каждой отдельной пары мал (примерно 0,27%), из-за большого числа пар общая вероятность резко увеличивается.
С увеличением группы вероятность совпадения растет еще стремительнее. Например, в компании из 50 человек шанс совпадения превышает 97%, а в группе из 70 человек — уже 99,9%. Этот парадокс наглядно показывает, как математика может противоречить нашей интуиции, и применяется в разных областях — от криптографии до анализа данных.
Фотография шанса уникального дня рождения для 23 человек:
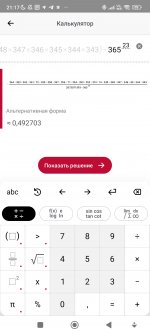
By Holmes
Суть в том, что вероятность совпадения растет гораздо быстрее, чем мы ожидаем. Вместо прямого подсчета шансов совпадения проще посчитать вероятность обратного — что у всех дни рождения разные. Для первого человека вероятность уникальности равна 100%, ведь других пока нет. Для второго — 364 из 365, потому что один день уже занят. Для третьего — 363 из 365, и так далее.
Если взять группу из 23 человек, то вероятность того, что все дни рождения разные, вычисляется как последовательное умножение: 365 умножить на 364, затем на 363, и так до 343, разделив каждый раз на 365. В итоге получается примерно 0,493, то есть 49,3%. Значит, вероятность хотя бы одного совпадения — это 100% минус 49,3%, то есть около 50,7%.
Почему так происходит? Дело в том, что с ростом числа людей количество возможных пар растет очень быстро. В группе из 23 человек можно составить 253 уникальные пары. Хотя шанс совпадения для каждой отдельной пары мал (примерно 0,27%), из-за большого числа пар общая вероятность резко увеличивается.
С увеличением группы вероятность совпадения растет еще стремительнее. Например, в компании из 50 человек шанс совпадения превышает 97%, а в группе из 70 человек — уже 99,9%. Этот парадокс наглядно показывает, как математика может противоречить нашей интуиции, и применяется в разных областях — от криптографии до анализа данных.
Фотография шанса уникального дня рождения для 23 человек:

By Holmes
